Overview Video
Abstract
We present a novel approach to model and reconstruct radiance fields. Unlike NeRF that uses pure MLPs, we consider the full volume field as a 4D tensor and propose to factorize the tensor into multiple compact low-rank tensor components for efficient scene modeling.
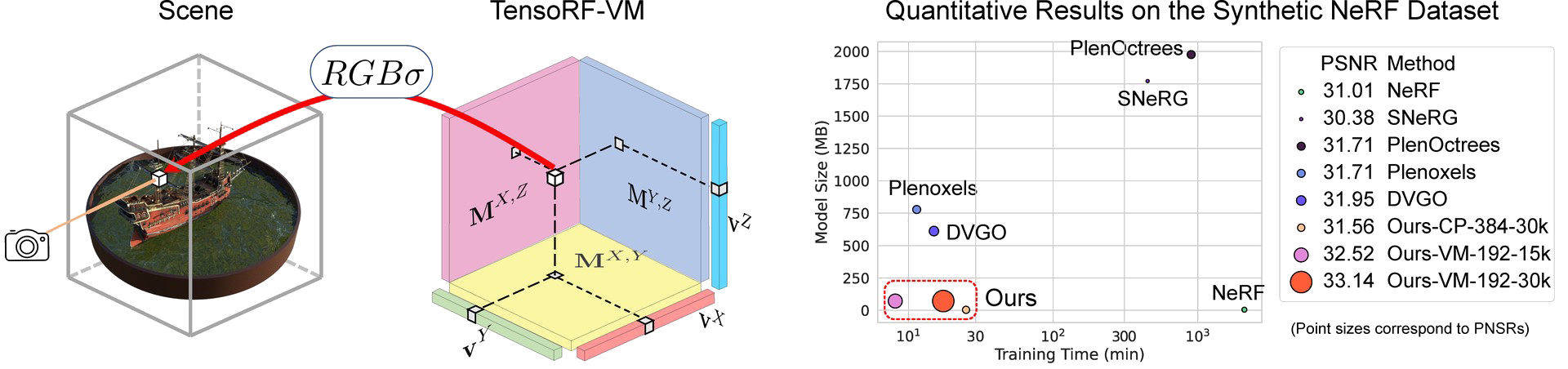
We model a scene (left) as a tensorial radiance field (right) using a set of vectors and matrices that describe scene appearance and geometry along their corresponding axes. These vector/matrix factors are used to compute volume density and view-dependent RGB color via vector-matrix outer products, leading to efficient radiance field reconstruction and realistic rendering. We demonstrate that TensoRF with CP decomposition can achieve fast reconstruction with better rendering quality and even a smaller model size (< 4MB) than NeRF. Moreover, TensoRF with VM decomposition can further boost our rendering quality to outperform previous state-of-the-art methods and reduce the reconstruction time (< 10min only with standard PyTorch implementation).
Method
We factorize radiance fields into compact components for scene modeling. To doso, we apply both the classic CP decomposition and a new vector-matrix (VM) decomposition; both are illustrated in following figure:

Left: CP decomposition, which factorizes atensor as a sum of vector outer products. Right: our vector-matrix decomposition, which factorizes a tensor as a sum of vector-matrix outer products. Please refer to our paper for more decomposition derails.
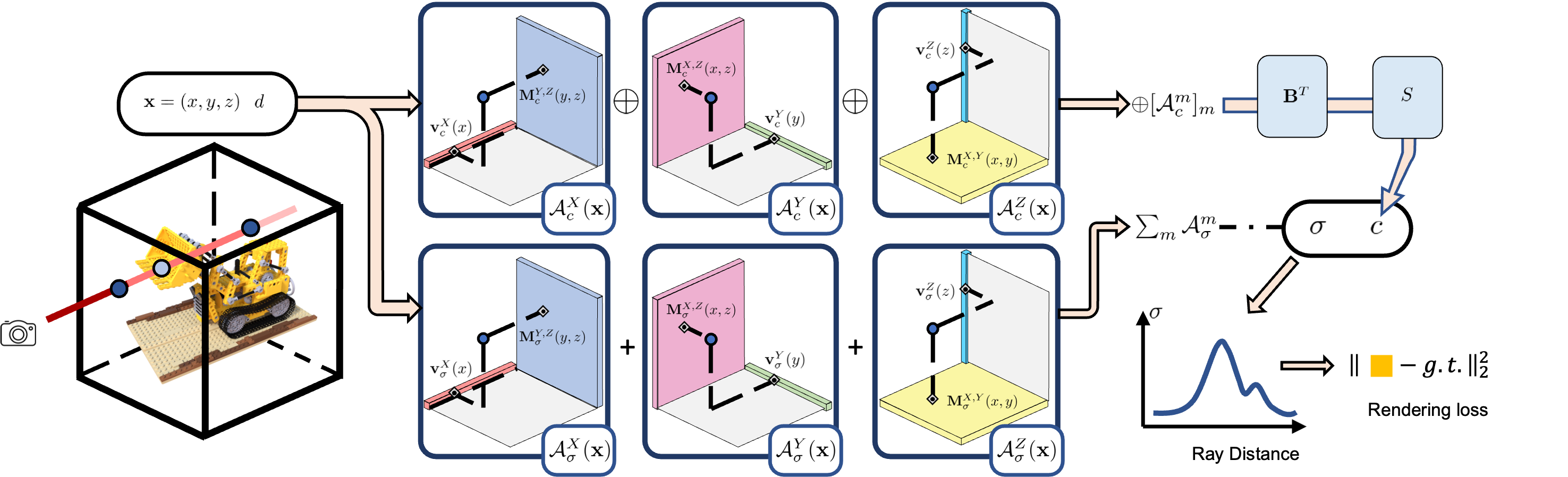
We now present our TensoRF representation and reconstruction. For each shading location x = (x,y,z), we use linearly/bilinearly sampled values from the vector (v)/matrix (M) factors to compute the corresponding trilinearly interpolated values of the tensor components. The density component values (Aσ(x)) are summed to get the volume density directly (σ). The appearance values (Ac(x)) are concatenated into a vector (⊕[Acm(x)]m) that is then multiplied by an appearance matrix (B) and sent to the decoding function S for RGB color (c) regression. The decoding function S can be a Spherical Harmonic (SH) function or a fully-connected network (FCN).
Super Fast Convergence
Given a set of multi-view input images with known camera poses, our tensorial radiance field is optimized per scene via gradient descent, minimizing an L2 rendering loss, using only the ground truth pixel colors as supervision.
Note that, unlike concurrent works Plenoxels and Instant-ngp that require customized CUDA kernels, our model’s efficiency gains are obtained using a standard PyTorch implementation.
Super Compact Memory Footprint
In contrast to previous works that directly reconstruct voxels, our tensor factorization reduces space complexity from O(n3) to O(n) (with CP) or O(n2) (with VM), significantly lowering memory footprint.
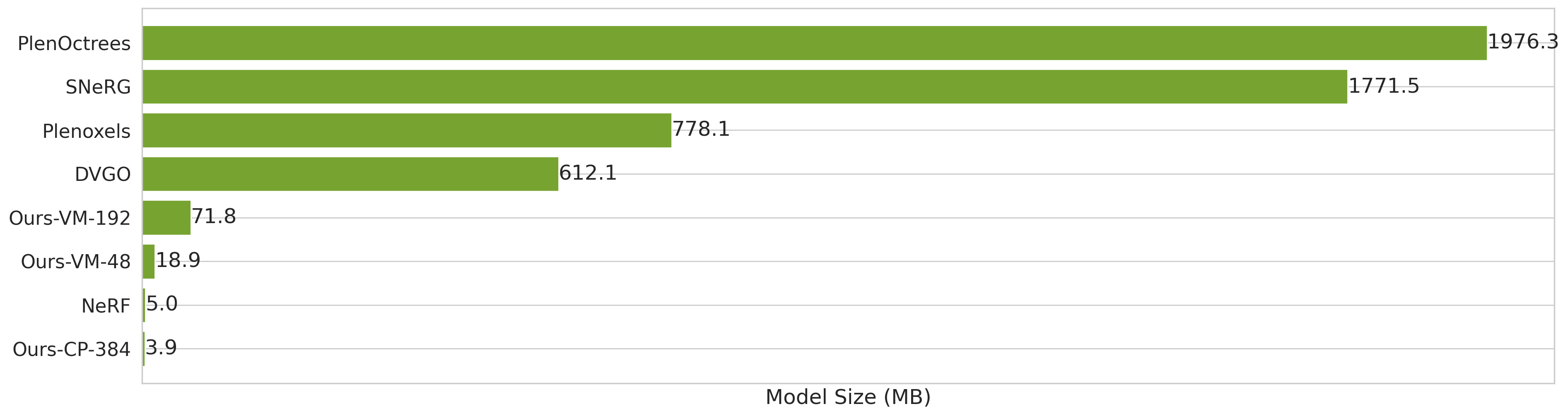
The above figure shows the checkpoint size on Synthetic-NeRF dataset (without compression), less always is more.
Super Vivid Details
Our approach can also achieve high-quality radiance field reconstruction for 360o objects and forward-facing scenes. All results without compression are available at OneDrive.
Visualization
Here we visualize the trained density basis of the Lego scene, the number of the basis is 16 for each dimension. We normalize the basis with min/max value along each dimension thus the brightness corresponds to their energy.
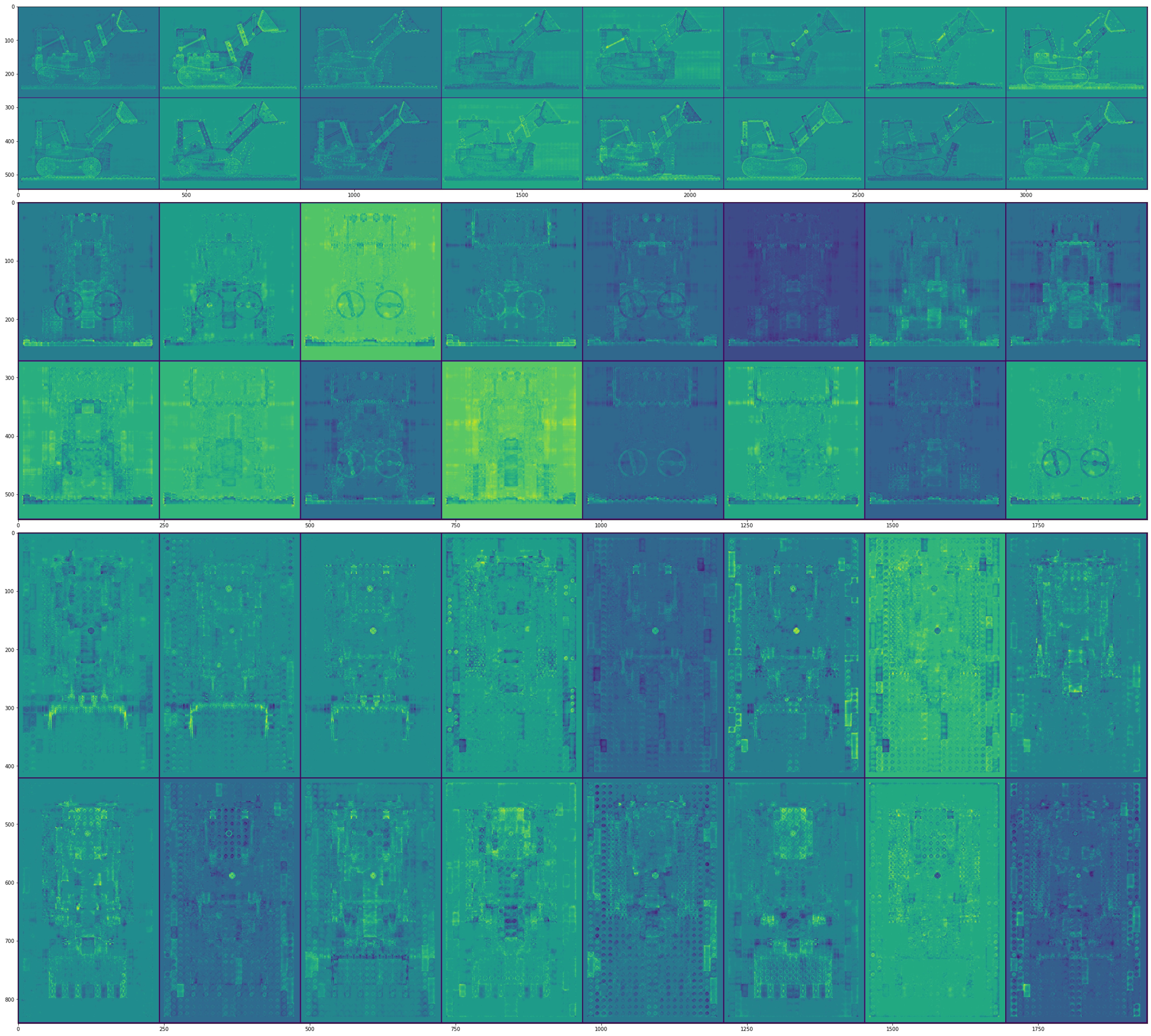
We can also convert the above density basis to a mesh using marching cubes.
Some concurrent works also focus on speeding up the training process or compact representation:
- Dense grid with a shallow MLP. DVGO
- Sparse grid — Plenoxels: Radiance Fields without Neural Networks. Plenoxels
- Hash — Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. iNGP
We would like to thank Yannick Hold-Geoffroy for his useful suggestion in video animation, Qiangeng Xu for providing some baseline results, and, Katja Schwarz and Michael Niemeyer for providing helpful video materials. This project was supported by NSF grant IIS-1764078 and gift money from VIVO.